Why did I pick that tutorial?
I was using Java (and started to learn it) this semester for my programming module. Since I would like to make some games, I was looking for making something graphical in Java. I thought it would be hard since I always use Eclipse IDE and I don't think it would support making a graphic output like HTML5 Canvas. So I tried looking for simple game (not like those current console and PC games) in Java, and that's when I found the tutorial. It was interesting, learning Java Swing, though in the end I matched my code with the given code (I retyped the code and tried to optimised here and there, but in the end it didn't work, so I matched back D: ).
Why did I have the idea of doing stuff outside school work when that time was crucial deadlines time?
Simply said, at least it is better than spending my time on Facebook when I can't focus.
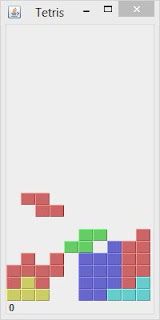
Screenshot
My Use of Java Swing
Apparently, in my programming class, there was this problem set on solving mazes. However, the mazes look like this:
On the maze above, we were asked to implement the maze with superpower of going through some wall. The broken wall is marked by XX (we need to implement the XX marking by ourselves while the maze printer for ## and PP was given). The two mazes pictures are of the same maze, with the previous one without superpower and this one with superpower of 5 (means can go through 5 walls).
So, naturally, there was a bonus question on the problem set to implement a better visual for the maze for 0 points. Well, I paused for a second and was thinking, would implementing better visual worth the 0 bonus points? Apparently, since I could reuse the code from the Tetris (though need more than just copying), I implemented the better visual (despite pressing homework, because making better visual is much more fun than doing my other homework). The result?
On the left is solving the maze without superpower while on the right is the one with superpower, with the maze and the source and destination points being the same as the ASCII maze above. Dots mark the path, blue blocks mark the walls and yellow blocks mark the destroyed wall. Quite neat, eh?
Apparently, it seems my tutor gave me some extra points for implementing this, not sure by mistake or not. Either way, it was fun :)
I had a trouble, though; there was another bonus question which has some marks allocated for it, and that is to generate the maze. I had brain freeze due to the piling homework that I could not implement it even though the algorithm is very much available on the Internet. :(
Why did I have the idea of doing stuff outside school work when that time was crucial deadlines time?
Simply said, at least it is better than spending my time on Facebook when I can't focus.
Screenshot
My Use of Java Swing
Apparently, in my programming class, there was this problem set on solving mazes. However, the mazes look like this:
On the maze above, ## means a wall, while PP is the path from the source (which in this case was (0,0)) to the destination (3,3). But when I saw the question, the printed maze was very confusing. And indeed, some people in the class had the same confusion as me.
On the maze above, we were asked to implement the maze with superpower of going through some wall. The broken wall is marked by XX (we need to implement the XX marking by ourselves while the maze printer for ## and PP was given). The two mazes pictures are of the same maze, with the previous one without superpower and this one with superpower of 5 (means can go through 5 walls).
================================
So, naturally, there was a bonus question on the problem set to implement a better visual for the maze for 0 points. Well, I paused for a second and was thinking, would implementing better visual worth the 0 bonus points? Apparently, since I could reuse the code from the Tetris (though need more than just copying), I implemented the better visual (despite pressing homework, because making better visual is much more fun than doing my other homework). The result?
 |  |
On the left is solving the maze without superpower while on the right is the one with superpower, with the maze and the source and destination points being the same as the ASCII maze above. Dots mark the path, blue blocks mark the walls and yellow blocks mark the destroyed wall. Quite neat, eh?
Apparently, it seems my tutor gave me some extra points for implementing this, not sure by mistake or not. Either way, it was fun :)
I had a trouble, though; there was another bonus question which has some marks allocated for it, and that is to generate the maze. I had brain freeze due to the piling homework that I could not implement it even though the algorithm is very much available on the Internet. :(


No comments:
Post a Comment